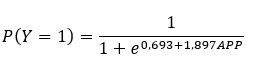ARTICULO ORIGINAL
REVISTA DE LA FACULTAD DE MEDICINA HUMANA 2021 - Universidad Ricardo Palma10.25176/RFMH.v21i3.3758
Evaluation of the discriminative capacity of anthropometric indicators and their predictive relationship of diabetes in health workers of the University Hospital of Guayaquil - Ecuador
Evaluación de la capacidad discriminativa de los indicadores antropométricos y su relación predictiva de diabetes en trabajadores de salud del Hospital Universitario de Guayaquil - Ecuador
Janet DR Gordillo-Cortaza1,2,a,b, Franklin Encalada-Calero1,3,a,c, Fatima V. Feraud-Ibarra1,a,d, Juan C. Roque-Quezada4,e, Rosa L. Quintana-Columbus1,e, Jennifer A. Plaza-Plaza5,e, Miguel A. Castro-Mattos6,a, Cinthya I. Falquez-García7,f, Dagmar Y. Meza-Solorzano1,g
1 Facultad de Medicina, Universidad de Guayaquil- Ecuador, Guayaquil, Ecuador
2 Universidad Nacional de Piura, Piura, Peru
3 Universidad Nacional de la Rioja, La Rioja, Argentina
4 Escuela Profesional de Medicina Humana, Universidad Privada San Juan Bautista Filial Chincha,
Ica, Peru
5 Compassion International Plenitud de Dios
6 Universidad Nacional de Barranca, Barranca, Peru
7 Hospital Universitario de Guayaquil, Guayaquil, Ecuador
a Full-time Professor
b PhD in Health Sciences
c University Master in Management
d Magister in medicine
e Surgeon
f Nutritionist
g Teaching Technician of the Nutrition Career
ABSTRACT
Objective: To evaluate the discriminative ability to predict diabetes with anthropometric and biochemical indicators and medical history. Methods: The sampling carried out was census and the sample consisted of 104 workers. A longitudinal study was carried out to evaluate the discriminative ability to predict diabetes with the anthropometric, biochemical, and antecedent indicators, using two models, the analysis of the ROC curves and binary logistic regression. Results: By analyzing the ROC curves, the abdominal circumference obtained greater predictive discriminative power (AUC = 0.747; p <0.001; CI: 0.624-0.870), compared to glycemia (AUC=0.749; p <0.001; CI: 0.645-0.852) and the waist-height index (AUC=0.737; p=0.001; CI: 0.638-0.836). Personal medical history is included in the logistic regression equation P(Y=1)=(1+e0,693+1,897APP)-1 to predict the risk of developing diabetes in the future. Conclusions: The abdominal circumference obtained the highest discriminative power, followed by the pathological history.
Keywords: Diabetes Mellitus; Forecasting; Risk (source: DeCs BIREME)
RESUMEN
Objetivo: Evaluar la capacidad discriminativa de predicción de diabetes con indicadores antropométricos, bioquímicos y antecedentes. Métodos: El muestreo realizado fue censal y la muestra estuvo conformada por 104 trabajadores. Se realizó un estudio longitudinal para evaluar la capacidad discriminativa de predicción de diabetes con los indicadores antropométricos, bioquímicos y antecedentes, mediante dos modelos, el análisis de las curvas ROC y regresión logística binaria. Resultados: Mediante el análisis de las curvas ROC, el perímetro abdominal obtuvo mayor poder discriminativo de predicción (AUC=0,747; p<0,001; IC: 0,624-0,870), en comparación a la glicemia (AUC=0,749; p<0,001; IC: 0,645-0,852) y el índice de cintura-talla (AUC=0,737; p=0,001; IC: 0,638-0,836). Los antecedentes patológicos personales se incluyen en la ecuación de regresión logística P(Y=1)=(1+e0,693+1,897APP)-1 para predecir el riesgo de tener diabetes en el futuro. Conclusiones: El perímetro abdominal obtuvo mayor poder discriminativo, seguido de los antecedentes patológicos personales.
Palabras Clave: Diabetes Mellitus; Predicción; Riesgo (fuente: DeCS BIREME).
INTRODUCTION
The use of anthropometric indicators to relate it to diabetes has gained relevance in the
academic field. Many investigations link anthropometric measurements and biochemical markers to predict
the onset of diabetes. A PURE study design (Population Health Research Institute) was carried out in
some communities in Colombia to evaluate the association between waist circumference, grip strength,
body weight, and age (1). Waist circumference was the leading risk factor for
a high MetS score.
A longitudinal study in children with type 1 diabetes mellitus, from 5 to 18 years of age in a
Hospital in the northwest of Brazil; to anthropometric measurements, triglyceride, and glycated
hemoglobin values were added; the triglyceridemic waist phenotype (CHTG), have a higher body mass index
and glycosylated hemoglobin with a significance of p <0.05 (2).
The waist circumference, measured in a horizontal plane, between the lower margin of the rib
and the upper edge of the iliac crest, according to the guidelines of the World Health Organization
(3), continues to show that it is a better predictor for diabetes than
body mass index (4).
The objective of the study was to evaluate the discriminative ability to predict diabetes
with anthropometric and biochemical indicators and antecedents. Anthropometric, biochemical, and
background indicators turn out to be good discriminators for predicting diabetes mellitus, as well
as having a good level of sensitivity and specificity (5).
METHODS
Design and study area
A longitudinal study to evaluate the discriminative ability to predict diabetes with anthropometric, biochemical, and antecedent indicators, using two models, the analysis of the ROC curves and binary logistic regression, in the health personnel of the Hospital Universitario de Guayaquil.
Population and sample
Since the objective of the study was to evaluate the discriminative capacity in anthropometric indicators in the hospital health employees and since the population was no greater than 200, it was decided to carry out a census-type sampling, including all workers who met the inclusion criteria (not having diabetes). The sample consisted of 104 health workers of both genders, from November 2020 to January 2021. Access was obtained to the electronic medical record contained in the database in the statistics service. In the analysis, personnel with a diagnosis of type 2 diabetes mellitus were excluded.
Variables and instruments
The study variables are the following: general data (age, gender, personal and family
pathological history, and as vital signs, normal blood pressure <130 mmHg systolic and <80 mmHg
diastolic) (6); anthropometric evaluation, by weight (kg), height (cm),
body mass index (BMI), values of 25–29.9 kg / m2 and ≥ 30 kg / m2, defined as overweight and
obesity; abdominal girth (cm), normal values for men <102 cm, women <88cm; Likewise, for the
waist-hip
index 0.8 in women and 1 in men, according to the World Health Organization (7), the waist-height index, a healthy level is considered lower than 0.5
(8); the percentage of body fat, an equation is made, Men: 63 - (20 x
height/circumference) vn: 18 - 24 and Women: 76 - (20 x height/circumference) vn: 25 - 31; the
height (cm) of the patient divided by the circumference of the waist (9).
Serological biomarkers; Total cholesterol (mg / dl), triglycerides
(mg / dl), and fasting glycemia (mg / dl), was made with the Trinder colorimetric reagent kits
(10) and as a lifestyle, physical activity.
Risk detection scales were used for the present analysis; both scales (with different
levels each) were dichotomized. On the FINDRISC scale, a score> 14 (11)
was considered as the cut-off line between high risk and low
risk; In the STOP-NIDDM risk-score for prediction at 2.5 years, a minimum of 10 points was
considered to determine high risk (12) (Tables 1 and 2 (11) (12).
Table 1. Findrisc Diabetes Risk Score Risk ScoreScore
| Total | Interpretation |
|---|---|
| Less than 7 points | Low-risk level |
| 7 to 11 points | Slightly high-risk level |
| 12 to 14 points | Moderate risk level |
| 15 to 20 points | High-risk level |
| More than 20 points | Very high-risk level |
Table 2. Individual prediction for diabetes STOP-NIDDM
| Points | Risk of DM (%) |
|---|---|
| 0 | 12,51 |
| 1 | 14,46 |
| 2 | 16,70 |
| 3 | 19,23 |
| 4 | 22,10 |
| 5 | 25,32 |
| 6 | 28,92 |
| 7 | 32,91 |
| 8 | 37,29 |
| 9 | 42,09 |
| 10 | 47,15 |
| 11 | 52,56 |
| 12 | 58,18 |
| 13 | 63,92 |
| 14 | 69,63 |
| 15 | 75,18 |
| 16 | 80,39 |
| 17 | 85,11 |
| 18 | 89,21 |
Procedure
The data collection was carried out through the electronic medical record prepared by the occupational medicine staff. These data obtained were entered into an Excel file, to later be processed into the program SPPS version 25 and the Diagnostic test calculator version 2010042101.
Statistical analysis
It was performed in two stages. First, all the variables were evaluated individually through the
ROC curves, comparing them with the dichotomized results of the FINDRISC test, being the determinant to
include as a relevant variable, the AUC measurement, and its CI. Using the Youden index, the results of
the chosen variables were dichotomized to classify them into two groups according to their
predictability of risk. The results were contrasted with a Gold Standard (dichotomized results of the
STOP - NIDDM test) and were obtained True positive and true negative through a confusion matrix.
Finally, with these values, the diagnostic test characteristics were obtained using the Diagnostic test
calculator version 2010042101 (13).
In a second stage, logistic regression was used, assuming as the dependent variable the
STOP-NDDIM score (Dichotomized for logistic regression: low risk <10=; high risk> 10) with 4
qualitative
and 13 quantitative variables at the beginning of the process. The choice of the relevant
independent variables was performed by bivariate correlation analysis between the dependent variable
and each independent variable. For qualitative variables, a test was usedvariables2, while for
quantitative, Student's t and Mann Witney's U tests were used. Then a univariate logistic regression
analysis was performed to choose the variables that had a better performance. Finally, a Wald
forward multivariate analysis was applied.
Ethical aspects
It is worth mentioning that, to have access to the database for the management of statistics and admissions, informed consent was requested from the highest authority of the Hospital.
RESULTS
There are many scales to predict diabetes, but the most used is the Findrisc scale, which allows
assessing the risk of developing the disease in 10 years, using a score greater than 14, which
represents a slightly high risk. With the ROC and AUC curves (reference test: the FINDRISC score, which
divides the sample into two groups, low risk (<14) and high risk (> 14)) of the following
anthropometric
indicators: Age, systolic pressure and diastolic, family and personal pathological history, physical
activity, glycemia, cholesterol, triglycerides, weight, height, BMI, abdominal circumference,
waist-hip index, waist-height index and percentage of body fat.
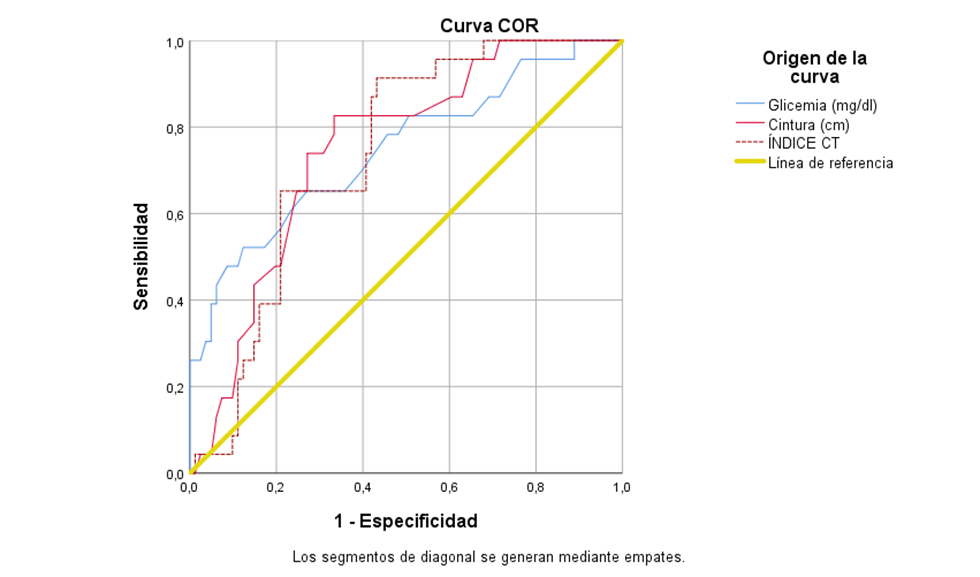
Better results were obtained with glycemia, abdominal circumference and waist-height index
(Figure 1). The abdominal circumference obtained greater discriminative power to predict diabetes
(AUC = 0.747; p <0.001; CI: 0.624-0.870), compared to glycemia (AUC=0.749; p <0.001; CI:
0.645-0.852)
and the index waist-height (AUC=0.737; p=0.001; CI: 0.638-0.836). Table 1 shows the Youden index,
the sensitivity and specificity of the tests.
Table 3.Cut points of the coordinates of the ROC curve.
| Parameter | Youden index | Cut point | Sensitivity | 1 - Specificity |
|---|---|---|---|---|
| Glycemia | 0.398 | 103.50 | 0.522 | 0.123 |
| Abdominal | 0.302 | 84.5000 | 0.957 | 0.654 |
| Waist-height index | 0.481 | 0.5477 | 0.913 | 0.432 |
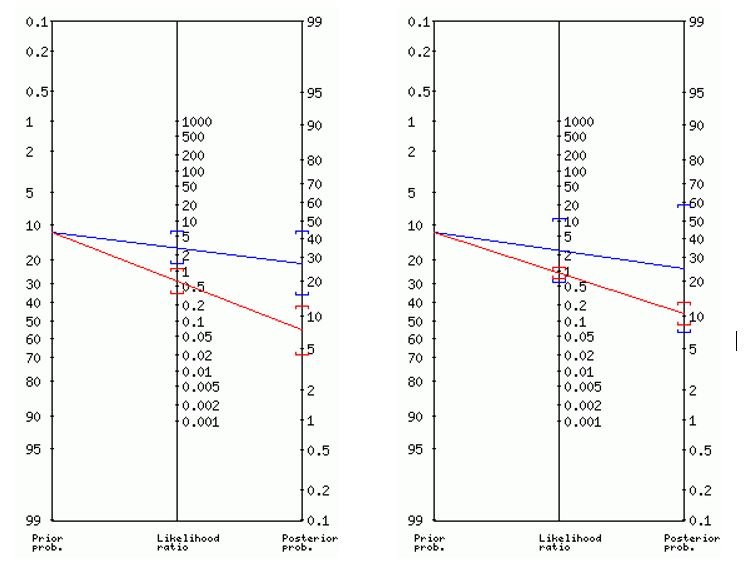
The cut points allowed dichotomizing the variables (those who had a high risk of having diabetes in the future and those that do not) to contrast them with a Gold Standard (the values of the STOP-NIDDM test, with at least 10 points to determine high risk) through a confusion matrix. The best results were obtained in the variable glycemia and abdominal circumference. For glycemia, True Positive= 6, False Positive= 16, False Negative= 6 and True Negative= 76 were obtained. In the same way, the following values were obtained for abdominal girth, TP = 2, FP = 6, FN = 10 and TN = 86. The Diagnostic test calculator with these values was used to obtain the diagnostic test characteristics for both variables (table 2).
Table 4. Characteristics of the diagnostic test.
| Characteristics | Glycemia | Abdominal | |
|---|---|---|---|
| Prevalence | circumference 0,115 | 0,115 | |
| Sensitivity | 0,495 | 0,167 | |
| Specificity | 0,828 | 0,935 | |
| + LR | 2,88 | 2,56 | |
| -LR | 0,61 | 0,89 | |
| Positive test | probability (95% CI) | ratio 2,88 (1,39-5,96) | 2,56 (0,58-11) Posterior |
| probability (95% CI) | 27% (15%-44%) a | 25% (7%-59%) c | |
| Negative test | probability ratio (CI, 95%) | 0,61 (0,35-1,08) | 0,89 (0,69-1,15) posterior |
| probability (95% CI) | 7% (4%-12%) b | 10% (8%-13%) d | |
Fagan nomograms for blood glucose (left) and abdominal girth (right) are shown in Figure 2.
In a second stage, it was evaluated which variables could enter the multivariate logistic
regression analysis. To the qualitative variables, the test was applied X2 (with the phi value) to
measure the association of the dependent variable with each independent variable. The variables with the
best results were: personal pathological history (APP, hereinafter: p = 0.001; phi = 0.312) and family
pathological history (APF: p = 0.042; phi = 0.2), while those ruled out were gender (p = 0.319) and
physical activity (p = 0.267).
In the case of quantitative variables, statistical tests were applied (Student's t for variables
with normal distribution and Mann-Whitney U for variables that did not have a normal distribution) to
determine the difference of means and medians between the groups formed by the dependent variable. The
variables chosen were systolic blood pressure (SBP, p = 0.018), diastolic blood pressure (DBP, p =
0.026), glycemia (p = 0.031), cholesterol (p = 0.032), triglycerides (p = 0.006). The rejected variables
were age (p = 0.256), BMI (p = 0.1), abdominal girth (p = 0.018 but Levene = 0.519), hip measurement (p
= 0.3), waist / hip ratio (p = 0.022 but Levene = 0.678), waist / height ratio (p = 0.079) and% fat (p =
0.759).
In a second stage, a univariate logistic regression was performed and they entered the final
model: APP (p = 0.04), APF (p = 0.07), SBP (p = 0.117), DBP (p = 0.035), glycemia (p = 0.039),
cholesterol (p = 0.077) and triglycerides (p = 0.034).
Multivariate logistic regression was applied to six variables APP, APF, DBP, glycemia,
cholesterol, and triglycerides, using the Wald forward method. The model performed 5 iterations until
the best was found, with a -2LL0 = 74.386 and afinal -2LL = 66.437. The omnibus test of the model’s
coefficients yields X2= 7.950 (p = 0.005), which allows evaluating the fit of the model. Cox and Snell's
R-squared is 0.074, while Nagelkerke's R-squared = 0.144. At the same time, the RL2= 0.10 and the
Pseudo-R2= 0.07.
Finally, the variable that enters the equation was APP (β = -1.897; p = 0.004; Exp (β) = 0.150;
95% CI = 0.042-0.542). Therefore, the logistic regression equation is finally defined as follows:
DISCUSSION
The World Health Organization (WHO) mentions that the number of people who have diabetes in
Latin America could reach 32.9 million by 2030 (14). In this sense, it is
important to determine the risk factors for Diabetes in health personnel through effective, sensitive,
and specific indicators. The present study shows similar results with a longitudinal study in health
workers that was carried out to relate the degree of occupation and risk factors for type 2 diabetes
(15).
With the analysis of the ROC curves, the abdominal circumference measurement had greater
discriminative power to predict diabetes (AUC = 0.747; p <0.001; CI: 0.624-0.870). This agrees with
various studies by Roos (16), Yoon (17),
Darsini (18), in which this indicator was effective in predicting risk.
In a cohort study with different cut-off points, the risk of acquiring diabetes was evaluated
(19), and it was determined that the abdominal circumference was the most
important.
The results of the ROC curve analysis and those of the diagnostic test calculator show that
the blood glucose test (0.522 and 0.495, respectively) has a medium level of sensitivity. This
result is similar to the measurement of the alteration of fasting glucose (> 100 mg/dl) in a health
insurance personnel in Korea to determine the risk of diseases (20).
When performing the bivariate correlation, those with the highest correlation were personal
pathological history (APP, hereinafter: p = 0.001; phi = 0.312) and family pathological history
(APF: p = 0.042; phi = 0.2). In turn, the multivariate logistic regression analysis showed that APPs
have predictive power (Nagelkerke's R squared = 0.144) (21). Although it
is true, this value is relatively low, it is important to note that this indicator allows predicting
the risk mathematically. In the same prediction model, it was found that APPs have a prediction
probability of 40%. (22).
LIMITATIONS OF STUDIES
One of the limitations is not having carried out the frequency of food consumption to investigate another prediction risk. Another limitation was not determining baseline insulin if it is directly related to abdominal girth and being another predictor for diabetes.
CONCLUSION
The analysis of the ROC curves shows that blood glucose and abdominal circumference are the best
predictors of diabetes. It is known that glucose is used to diagnose the presence of diabetes in
patients. For its part, the abdominal circumference is an effective indicator to predict diabetes, as
shown in this study and others carried out in Latin America and the Caribbean latitudes.
Multivariate logistic regression analysis places family medical history as an important variable
when predicting the probability of having diabetes in the future. The difference between this equation
with the FINDRISC tests and similar ones is that the equation gives a probability as a single variable.
In contrast, the other tests require lengthy questionnaires and measurements of many variables.
Therefore, a logistic equation is more versatile when it comes to forecasting probabilities. The best
predictors of diabetes risk are glycemic index, abdominal circumference, and personal medical history,
each with its potential, depending on the approach with which the test is used.
Author’s contributions: The authors participated in the structuring of concepts, project
design, collection and data interpretation, results in analysis and manuscript preparation
Funding sources: Self-financed
Declaration of conflict of interest: The authors declare no conflict of interest
Received: March 16, 2021
Approved: May 21, 2021
Correspondence: Janet Del Rocio, Gordillo Cortaza
Address: Km 11,5 vía a la Costa. Urb Belo Horizonte. Guayaquil –
Ecuador
Telephone: 593-993130520
Email: janetgordillo28@gmail.com
REFERENCES