ARTÍCULO DE REVISIÓN
REVISTA DE LA FACULTAD DE MEDICINA HUMANA 2020 - Universidad Ricardo PalmaDOI 10.25176/RFMH.v21i1.3069
ESTUDIOS TRANSVERSALES
CROSS-SECTIONAL STUDIES
Cvetkovic-Vega, A1, Jorge L. Maguiña2, Alonso Soto1,3, Jaime Lama-Valdivia1,4, Lucy E. Correa López1,5
1Instituto de Investigación en Ciencias Biomédicas, Universidad Ricardo Palma, Lima, Perú.
2Universidad Continental, Lima, Perú.
3Departamento de Medicina. Hospital Nacional Hipólito Unanue, Lima, Perú.
4Servicio de Geriatría. Hospital Nacional Hipólito Unanue, Lima, Perú.
5Facultad de Medicina Humana, Universidad Ricardo Palma, Lima-Perú.
Los estudios observacionales transversales pueden ser de tipo descriptivos o también analíticos dependiendo del objetivo general. Este diseño es rápido, económico y permite el cálculo directo de la prevalencia de una condición. Además, la relación de temporalidad entre la exposición y el efecto son medidas de forma simultánea en un único período, no siendo posible identificar una direccionalidad en la temporalidad. Cuando estos estudios persiguen un objetivo general analítico, la medida de asociación es la Razón de Prevalencias (RP), especialmente cuando la prevalencia del efecto es mayor o igual a 10% o el Odds Ratio (OR) cuando la prevalencia es baja. Para cuantificar esta asociación pueden utilizarse diferentes modelos de regresión como el binomial log o Poisson log, incluyendo los modelos lineales generalizados. Cuando la medida de asociación a utilizar es el OR, el modelo más comúnmente empleado es la regresión logística múltiple.
Palabras Clave: Transversal, Observacional, Analítico, Diseño, Estudios. (Fuente: DeCS BIREME)
ABSTRACT
Cross-sectional studies are epidemiological design which can be considered as descriptive or analytical designs depending on the general objective. This is a quickly and economical design and allows to calculate the prevalence of a condition. Also, the relationship of temporality between the exposition and the outcome is being measured simultaneously on a unique period, not being possible to identify a directionality in the temporality. When there is an analytic objective, the association measure used is the Prevalence Ratio (PR), specially when the prevalence of the outcome is more or equal to 10% or the Odds Ratio (OR) when that prevalence is lower. To quantify this association different regression models like Binomial log or Poisson log can be used, including generalized lineal models. If the association measure is OR, the most common used model is the multiple logistic regression.
Key words: Cross-sectional, Observational, Analytic, Design, Studies. (Source: MeSH NLM)
Los estudios observacionales se definen a partir de la ausencia de intervención del investigador en el desenlace que desea evaluar. Estos diseños pueden ser de tipo descriptivo en los cuales se incluyen los estudios transversales y los estudios de cohorte descriptivos; o también ser de tipo analítico incluyendo a los casos controles, los estudios cohorte clásico y los transversales(1). El elemento clave que define a un estudio transversal es la evaluación de un momento específico y determinado de tiempo, en contraposición a los estudios longitudinales que involucran el seguimiento en el tiempo. Tradicionalmente, los estudios transversales han sido considerados útiles para la determinación de la prevalencia de una condición, de ahí la sinonimia utilizada como “estudios de prevalencia”. Sin embargo éstos pueden también evaluar la asociación entre dos o más variables, es decir, tener un enfoque analítico(2) siendo una alternativa interesante para explorar asociaciones de manera preliminar o en escenarios de recursos limitados.
Para entender esta idea, resulta importante tener muy en claro el concepto de temporalidad entre las variables independientes o covariables según sea el caso, y la dependiente (desenlace). Si bien en los diseños observacionales analíticos de tipo cohorte, la temporalidad marca una dirección que va en el sentido de exposición hacia efecto, y en los casos-controles la dirección va del efecto hacia la exposición, en los estudios transversales que persiguen objetivos analíticos la exposición y el efecto se miden en simultáneo(3). A partir de ello, se entiende además que el sentido transversal corresponde a una única medición en un lapso, y que en ese contexto planeamos analizar la relación de asociación entre variables.
Adicionalmente, en la literatura científica estos estudios se denominan transversales (cross-sectional studies) sin hacer distinción entre descriptivos y analíticos, e identificando dicha distinción a partir del objetivo general del estudio. Sin embargo, para fines educativos y de formación en pregrado podría ser posible hacer esta distinción siempre resaltando su utilidad e indicando su uso adecuado en la literatura.
MEDIDAS DE ASOCIACIÓN
La medida de asociación tradicional de los estudios transversales analíticos es el Odds Ratio (OR). Sin embargo en los últimos años se ha utilizado crecientemente la Razón de Prevalencias (RP), la cual se define en términos de “cuántas veces es más probable que los individuos expuestos presenten la enfermedad o condición respecto a aquellos individuos no expuestos”(4). A continuación, presentaremos la similitud matemática de la RP con el Riesgo Relativo (RR) , partiendo del segundo. Sean un desenlace Y y un factor de exposición X. En una tabla de 2x2 graficaremos (Figura 1):

Figura 1. Tabla de 2x2 para cálculo de RR de un desenlace Y a partir de una exposición a un factor X
En el cálculo del RR que corresponde a los diseños de cohorte, se calcula el riesgo de que tras la exposición a un factor X se registre un caso nuevo de desenlace Y, por lo que se calculará el RR a partir de la incidencia acumulada(5,6) del desenlace Y (Iexp) en el grupo de expuestos comparándola con la incidencia acumulada en el grupo de no expuestos (Ino exp). Esto puede apreciarse a continuación:
La incidencia acumulada en los expuestos (Iexp) a partir de la Figura 1 se calculará así:
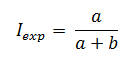
La incidencia acumulada en los no expuestos (Ino exp) a partir de la Figura 1 se calculará así:
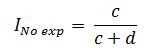
Finalmente, el RR se calculará a partir de la razón entre la incidencia acumulada en los expuestos y en los no expuestos:
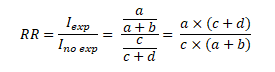
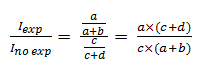
Habiendo esclarecido esto, pasaremos a calcular la RP demostrando la similitud matemática con el RR. Antes de presentar la Figura 2, resulta crucial entender que bajo un criterio epidemiológico los estudios de tipo Cohorte están relacionados con la incidencia acumulada, es decir, los casos nuevos de una enfermedad determinada mientras que los estudios transversales no se relacionan con este concepto sino con la frecuencia o prevalencia de un evento utilizando el total de casos (tanto nuevos como antiguos) dentro de una única medición. Sean un desenlace Y y la exposición a un factor X medidos simultáneamente en un momento único. En una tabla de 2x2 graficaremos (Figura 2):
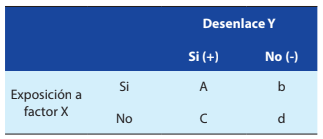
Figura 2. Tabla de 2x2 para cálculo de la RP de un desenlace Y a partir de la exposición a un factor X medidos simultáneamente
En el cálculo de la RP se calcula la razón de la prevalencia del desenlace Y en el grupo donde está presente el factor X (Pexp) sobre la razón de la prevalencia del desenlace Y en el grupo donde no está presente el factor X (Pno exp). Por lo tanto:
La prevalencia del desenlace Y en el grupo donde está presente el factor X medidos simultáneamente (Pexp) a partir de la Figura 2 se calculará así:
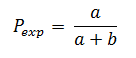
La prevalencia del desenlace Y en el grupo donde no está presente el factor X medidos simultáneamente (Pno exp) a partir de la Figura 2 se calculará así:
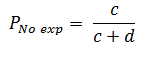
Finalmente, la RP se calculará a partir de la razón entre la prevalencia en los expuestos y en los no expuestos:
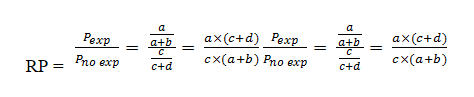
Por lo tanto, la fórmula matemática para ambos casos es la misma pero los conceptos epidemiológicos no son los mismos. Mientras que en las cohortes el RR utiliza la incidencia acumulada, en la RP se utiliza la prevalencia.
Explicado esto, introducimos el siguiente concepto: la medida de asociación en un estudio transversal puede ser o bien la RP u OR (utilizado tradicionalmente en los estudios de casos-control) y la elección de la mejor medida de asociación depende de la observación inicial de la prevalencia del desenlace en el estudio.
A partir de la observación de la prevalencia del desenlace, existen diferentes comunicaciones en la literatura académica que estiman un punto de corte válido para seleccionar el uso de RP u OR teniendo como criterio que por encima ese punto de corte el uso de OR sobreestimaría al RP, concepto similar al utilizado en el caso del RR(4,7). Se considera que a partir de una prevalencia de desenlace mayor o igual al 10% debe utilizarse la RP como medida de asociación adecuada para el estudio transversal puesto que de utilizarse el OR se sobreestimaría el valor de la RP(8). Por debajo del 10%, podría utilizarse el OR, sin embargo, se recomienda el uso de RP para estudios transversales que persiguen objetivos analíticos(8-10). A continuación, se presenta la Figura 3, que si bien inicialmente ha sido diseñada para comparar OR vs RR, ya se explicó que matemáticamente el cálculo de RR y RP es semejante difiriendo en su interpretación epidemiológica y por lo tanto, el efecto presentado es válido y extrapolable para una comparación de OR vs RP.
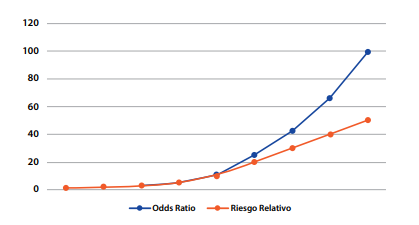
Figura 3. Comparación del OR y RR / RP a partir de la prevalencia del desenlace*
*Tomada de: Soto A, Cvetkovic-Vega A. Estudios de casos y controles. Rev Fac Med Humana 2020, 20(1):138-43
Otro de los criterios para definir el uso de OR o RP es la posible relación de casusa a efecto entre las variables. Así, cuando se tiene una suposición razonable sobre la variable considerada como exposición y la variable considerada como desenlace, es conveniente la comparación de prevalencia de efecto entre expuestos y no expuestos y el cálculo del RP. Cuando no se tiene clara la relación causal entre las variables, el OR tiene la ventaja de mantener el mismo valor numérico independientemente de su ubicación en la tabla de contingencia. Por el contrario, la RP va a tomar valores diferentes de acuerdo a si una variable es considerada como exposición o efecto.
Para ilustrar los conceptos previos comparemos algunos factores asociados a sepsis neonatal temprana a partir de una prevalencia del 30% de ésta y siendo los factores por considerar la edad gestacional, ser gestante añosa, los controles prenatales y la ruptura prematura de membranas de más de 18 horas. A continuación, presentamos los datos obtenidos a partir de una tesis de pregrado de medicina en la cual se elabora una comparación de los cálculos de la RP y OR en sus formas cruda (RPc y ORc) y ajustada (RPa y ORa) (Tabla 1).
Tabla 1. Comparación entre la RP y el OR en el análisis bivariado
| Sepsis Neonatal Temprana | ||||
| Razón de Prevalencia cruda (IC95%) | Odds Ratio crudo (IC95%) | Razón de Prevalencia ajustada (IC95%) | Odds Ratio ajustado (IC95%) | |
| Edad gestacional | 0,83 (0,76-0,9) | 0,71 (0,62-0,81) | 0,87 (0,8-0,96) | 0,76 (0,65-0,89) |
| Gestante añosa | 1,64 (1,4-2,35) | 2,07 (1,2-3,55) | 1,77 (1,13-2,75) | 3,9 (1,91-8,01) |
| Suficiencia de controles prenatales | 0,8 (0,76-0,85) | 0,66 (0,58-0,76) | 0,81 (0,74-0,89) | 0,62 (0,52-0,73) |
| Ruptura Prematura de membranas >18h | 2,55 (1,82-3,58) | 4,69 (2,52-8,72) | 2,34 (1,5-3,68) | 7,95 (3,56-17,74) |
Para una prevalencia del 30% para la variable desenlace (Sepsis Neonatal Temprana) se observan diferencias pequeñas entre los resultados de la RP y OR cruda y ajustada para edad gestacional y la suficiencia de controles prenatales. Sin embargo, la diferencia va aumentando cuando se compara el intervalo para la RPa y Ora en la variable gestante añosa, y se hace más evidente en la variable Ruptura Prematura de Membranas 18h donde se evidencia una sobreestimación de utilizarse el OR y no la RP.
CONSIDERACIONES PARA EL DISEÑO
Eficiencia estadística
En un estudio transversal no se aplica el concepto de eficiencia estadística pues se mide de forma simultánea la exposición y el resultado.
Cálculo del tamaño muestral
Es importante entender que en el tamaño muestral para los estudios transversales descriptivos y los analíticos se emplean fórmulas diferentes puesto que los primeros representan a una proporción única (representada por la prevalencia de un evento) y los segundos, a dos o más proporciones (representada por presencia o ausencia de la exposición de un factor y en un desenlace determinado).
Para estudios transversales descriptivos
En estos estudios se utiliza la fórmula de tamaño muestral para una sola proporción con un nivel de confianza y un margen de error determinados. Esta fórmula puede ser despejada y utilizarse en dos contextos: para una población cuyo tamaño es conocido y una cuyo tamaño no lo es(11).
En el caso de una población cuyo tamaño es conocido, la fórmula a utilizar es:
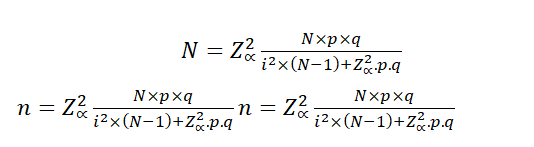
Donde:
n: Tamaño de la muestra
N: Tamaño de la población
p: Prevalencia del evento de estudio
q: 1-p
Zα: Cuando α=0.05, el valor en la distribución gaussiana es igual a 1,96
i: Tolerancia al error (Si es 95%, su valor es de 5%).
Para una población cuyo tamaño no es conocido, la fórmula a utilizar es:
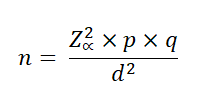
Donde:
n: Tamaño de la muestra
p: Prevalencia del evento de estudio
q: 1-p
Zα: Cuando α=0.05, el valor en la distribución gaussiana es igual a 1,96
d: Tolerancia al error (Si es 95%, su valor es de 5%).
Para estudios transversales analíticos
En este tipo de estudios existen diferentes formas de realizar el cálculo del tamaño muestral, sea por ejemplo mediante el uso de las razones de prevalencia o a través de diferencias de proporciones. De forma académica y sencilla, utilizaremos esta última.
A continuación, se presenta la fórmula general adaptada y teniendo en cuenta la Figura 2:
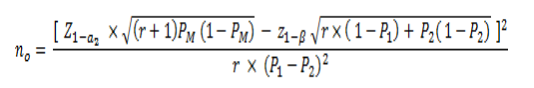
Figura 4. Fórmula estadística para el cálculo de tamaño muestral en un estudio transversal de objetivo principalmente analítico
Donde:

Cálculo del tamaño muestral
Al realizar este cálculo, no se refiere al tamaño muestral total el cual deberá ser repartido entre el grupo con evento Y positivo y el de evento Y negativo siguiendo la razón calculada. Se recuerda al lector que todo cálculo de tamaño muestral puede hacerse de forma práctica y sencilla mediante el uso de programas estadísticos y plataformas online que poseen calculadoras para este fin.
Elección de grupos positivos y negativos para un desenlace
A diferencia de otros estudios, en estos diseños no puede aplicarse el criterio de seleccionar grupos (semejante a los criterios utilizados en los casos y los controles)(12) puesto que se explora a toda una población y se cuantifica la cantidad de expuestos y no expuestos así como las personas con o sin el desenlace.
ANÁLISIS ESTADÍSTICO
El cálculo de la RP como se ha mencionado previamente es análogo al cálculo del RR. Para el análisis multivariado en el que la RP se ajusta a posible variables confusoras, la RP para una relación determinada entre variables junto con su intervalo de confianza y valor p puede ser calculada de distintas maneras como por ejemplo mediante la regresión de Poisson con varianzas robustas, o la regresión log-binomial(13). Otro de los métodos también son modelos lineales generalizados con familia binomial y función de enlace log. En el caso que se considere conveniente el uso de OR es apropiado utilizar regresión logística.
VENTAJAS Y DESVENTAJAS
Como en todo estudio, ningún diseño es perfecto puesto que tiene limitaciones que hay que identificarlas adecuadamente y desarrollar una buena práctica en investigación que permita comunicarlas a los demás investigadores facilitando de esta forma la comprensión y replicación de nuestro estudio.
Los estudios transversales que persiguen objetivos principalmente analíticos suelen ser estudios que aportan evidencia preliminar en lo relacionado con la investigación de la existencia de asociaciones entre variables, considerándolos como el primer peldaño en los niveles de evidencia del grupo de los observacionales analíticos. La principal limitación, que a su vez es la principal característica de este tipo de estudios, es la imposibilidad de determinar una secuencia temporal clara entre la variable dependiente y la(s) variables independientes o covariables. Esto es debido a que la medición de ambos tipos de variables se hace de manera simultánea.
Estos estudios son considerados relativamente sencillos y con costos pequeños, con fácil y rápida ejecución permitiendo tener una aproximación preliminar que puede ser útil para la toma de decisiones rápidas. Otra de sus fortalezas es que son útiles para medir la prevalencia. Sin embargo, es importante considerar sesgos clásicos como el de selección o también el sesgo de recuerdo. Por último, amerita resaltar que de no considerarse 10% como punto de corte para la frecuencia del desenlace y uso de RP es probable que se sobreestime la medida de asociación al utilizarse el OR, lo cual ya fue descrito previamente.
CONCLUSIÓN
Los estudios observacionales de tipo transversal pueden clasificarse en descriptivos o analíticos a partir del objetivo general del estudio. Los de índole analítica poseen una hipótesis de investigación en la cual se evalúa la presencia de una asociación entre variables de tipo cualitativa o también cuantitativas. La principal característica de este tipo de estudio es que tanto la variable desenlace como exposición son medidas de forma simultánea, por lo que no se puede establecer una adecuada relación de temporalidad. Estos estudios aportan un nivel de evidencia preliminar en relación con la asociación entre variables en comparación con los casos-controles y las cohortes. Se recomienda que los investigadores tengan en cuenta los conceptos relacionados a este tipo de estudio para evitar confusiones con los estudios de casos-controles a nivel de identificación del diseño y la secuencia temporal entre exposición y desenlace, uso de medida de asociación según prevalencia del desenlace y cálculo de tamaño muestral.
Contribuciones de Autoría: ACV contribuyó con la concepción y diseño, redacción y revisión crítica, aprobación final y asesoría estadística. JLM contribuyó con la redacción y revisión crítica, aprobación final y asesoría estadística. AS contribuyó con la concepción y diseño, redacción y revisión crítica, aprobación final y asesoría estadística. JLV contribuyó con redacción y revisión crítica, y aprobación de versión final. JDV contribuyó con la redacción y revisión crítica, y aprobación de versión final.
Financiamiento: Autofinanciado.
Conflictos de intereses: Los autores declaran no tener conflictos de interés.
Recibido: 18 de Junio de 2020
Aprobado: 17 de Julio de 2020
Correspondencia: Aleksandar Cvetković Vega.
Dirección: Jirón Bronsino 307, San Borja, Lima-Perú.
Teléfono: + 51 964982676
Correo: acvetkovic@continental.edu.pe
REFERENCIAS BIBLIOGRÁFICAS
