RESUMEN

Introducción: En los últimos meses, los investigadores han venido empleando métodos matemáticos para poder pronosticar el número de casos de COVID-19 en todo el mundo. Objetivo: Estimar un modelo Autorregresivo Integrado de Medias Móviles (ARIMA) para el análisis de series de casos de COVID-19, en Perú. Métodos: El presente estudio se basó en un análisis de series temporales univariante; los datos utilizados se refieren a la cantidad de casos nuevos acumulados de COVID-19 del 06 de marzo al 11 de junio de 2020. Para el análisis del ajuste del modelo se utilizaron los coeficientes de autocorrelación (ACF), el contraste de raíces unitarias de Dickey-Fuller Aumentado (ADF), el Criterio de Información Bayesiano Normalizado (BIC Normalizado), el error porcentual medio absoluto (MAPE) y el test de Box-Ljung. Resultados: El pronóstico de casos de COVID-19, entre el 12 de junio al 11 de julio de 2020 oscila entre 220 596 a 429 790. Conclusiones: Los resultados obtenidos con el modelo ARIMA, comparados con los datos observados, muestran un ajuste adecuado de los valores; y aunque este modelo, de fácil aplicación e interpretación, no simula el comportamiento exacto en el tiempo puede considerarse una herramienta simple e inmediata para aproximar el número de casos.

Palabras Clave: Pronóstico; Pandemias; Coronavirus (Fuente: DeCS BIREME)

ABSTRACT

Introduction: In recent months, researchers have been using mathematical methods to predict the number of COVID-19 cases worldwide. Objective: To estimate an Integrated Autoregressive Moving Average model (ARIMA) for the analysis of series of COVID-19 cases, in Peru. Methods: The present study was based on a univariate time series analysis; The data used refer to the number of new accumulated cases of COVID-19 from March 6 to June 11, 2020. For the analysis of the fit of the model, the autocorrelation coefficients (ACF), the unit root test of Augmented Dickey-Fuller (ADF), the Normalized Bayesian Information Criterion (Normalized BIC), the absolute mean percentage error (MAPE) and the Box-Ljung test. Results: The prognosis for COVID-19 cases, between June 12 and July 11, 2020 ranges from 220 596 to 429 790. Conclusions: The results obtained with the ARIMA model, compared with the observed data, show an adequate adjustment of the values; And although this model, easy to apply and interpret, does not simulate the exact behavior over time, it can be considered a simple and immediate tool to approximate the number of cases.

Key words: Forecasting; Pandemics; Coronavirus (fuente: MeSH NLM).

INTRODUCCIÓN

El nuevo coronavirus (coronavirus 2 del síndrome respiratorio agudo severo-SARS) fue reportado en el mes de diciembre de 2019 en la ciudad de Wuhan-China, con la aparición de varios casos de neumonía de etiología desconocida que causó problemas respiratorios agudos severos ^(1-7). Este se transmite por inhalación de gotitas respiratorias, contacto cercano con el individuo infectado, y contacto con superficies u objetos contaminados ^(1,8).

El 11 de marzo de 2020 la Organización Mundial de la Salud (OMS) declaro al COVID-19 como una pandemia ⁽⁹⁾. Los casos se incrementan a nivel mundial, incluido el Perú, donde el primer caso se anunció el 6 de marzo; siendo al 12 de julio, el número total de casos confirmados, de 326 326 ⁽¹⁰⁾.

Existe una gran preocupación de la capacidad de respuesta del sistema de salud peruano para afrontar efectivamente a las necesidades de las personas con COVID-19 ya que el número de casos se incrementa y a pesar de todas las medidas dadas por el gobierno, este no se detiene; más aún que el gobierno “abrió las puertas" a la población a una “nueva normalidad”.

Los modelos matemáticos son usados para entender las transiciones epidemiológicas críticas ^(11-14), y en los últimos meses, los investigadores han venido empleando métodos matemáticos para poder pronosticar el número de casos de COVID-19 en todo el mundo. El Método Autorregresivo Integrado de Medias Móviles (ARIMA) es el que más se ha utilizado para realizar pronósticos, tal es el caso de los propuestos por Singh RK et al ⁽¹¹⁾, para Estados Unidos, España, Italia, Francia, Alemania, el Reino Unido, Turquía, Irán, China, Rusia, Brasil, Canadá, Bélgica, los Países Bajos y Suiza; por Ceylan Z ⁽¹⁵⁾, para Italia, España y Francia; por Moftakhar L y Seif M⁽¹⁾, para Irán; por Benvenuto D et al⁽¹⁶⁾, para Italia; por Yousaf M et al⁽¹⁷⁾, para Pakistán; por Hiteshi Tandon⁽¹⁸⁾ y Rishabh Tyagi et al⁽¹⁹⁾, para India y por Perone G⁽²⁰⁾, para Italia.

Las series temporales constituyen colecciones de datos en un período de tiempo en los cuales se observan las tendencias o patrones para pronosticar algunos valores futuros ⁽²¹⁾. El modelo ARIMA cuenta con tres principales parámetros; el parámetro p: asociado a la parte autorregresiva (AR); el cual es el número de diferencias que hay que tomar a la serie para que sea estacionaria; el parámetro d: asociado a la parte integrada (I) y; el parámetro q: asociado a la parte de media móvil (MA); el cual es el valor actual de una serie, que se define como una combinación lineal de errores pasados^(11,12,18).

Para estimar un modelo ARIMA se utiliza la metodología de Box-Jenkins^(11,22-23), la cual consta de 4 etapas: la identificación: que consiste en identificar el modelo que tentativamente se puede considerar; la estimación: que consiste en estimar los parámetros del modelo considerado tentativamente; la validación: que consiste en realizar contrastes de diagnóstico para comprobar si el modelo se ajusta a los datos y; la predicción: que consiste en obtener pronósticos en términos probabilísticos de los valores futuros y en la cual se evalúa la capacidad predictiva del modelo⁽²⁴⁾.

Una de las preocupaciones en el Perú y en cualquier otro país, es saber cuántas personas se infectarán con COVID-19 en el tiempo; y esta se podría responder con modelos predictivos⁽²⁵⁾; por lo tanto, el presente estudio tuvo como objetivo, estimar un modelo Autorregresivo Integrado de Medias Móviles (ARIMA) para el análisis de series de casos de COVID-19, en Perú, con el fin de buscar una aproximación entre los resultados obtenidos con el modelo y los datos observados.

MÉTODOS

Diseño y área de estudio

El presente estudio se basó en un análisis de series temporales univariante, descriptivo, transversal, retrospectivo, realizado en Perú, con la cantidad de casos nuevos diarios confirmados de COVID-19, entre el 06 de marzo y 11 de junio del 2020.

Población y muestra

Los datos utilizados se refieren a la cantidad total de casos nuevos diarios confirmados de COVID-19 entre el 06 de marzo y 11 de junio del 2020.

Variables e instrumentos:

Los datos provienen de la Sala Situacional COVID 19-Peru, del Instituto Nacional de Salud y Centro Nacional de Epidemiologia, Prevención y Control de Enfermedades del Ministerio de Salud⁽¹⁰⁾; los cuales sirven para obtener la precisión del pronóstico de la propagación del COVID-19.

Procedimientos

Los datos sirvieron para obtener los pronósticos del número de casos de los siguientes 30 días, desde del 12 de junio hasta el 11 de julio de 2020, creando una trayectoria proyectada de estos casos, para posteriormente compararlos con los casos observados en el periodo de tiempo indicado.

Análisis estadísticos

El método de series temporales utilizado para el pronóstico de los casos de COVID-19 fue el Autorregresivo Integrado de Medias Móviles de orden (p, d, q) o ARIMA (p, d, q). La construcción del modelo se realizó de forma iterativa siguiendo las 4 etapas de la metodología de Box-Jenkins^{(11, 22-24)} 1-Identificacion: en la cual se determinó la transformación estacionaria de la serie para obtener el modelo apropiado, mediante el análisis de los coeficientes de autocorrelación (ACF), y el contraste de raíces unitarias de Dickey-Fuller Aumentado (ADF); 2-Estimación: en la cual, mediante la elección de las ordenes p, d, q apropiadas, se ajustó el modelo a la serie temporal, obteniéndose el modelo ARIMA (0,2,9); 3-Validacion: en la cual se analizó si el modelo era apropiado, y se valoró con el Criterio de Información Bayesiano Normalizado (BIC Normalizado), el error porcentual medio absoluto (MAPE) y la prueba de ruido blanco o test de Box-Ljung; 4-Predicción: en la cual se generó los pronósticos del número de casos de los siguientes 30 días; para luego compararlos con los casos observados. El programa estadístico que se utilizó para el análisis de la serie temporal fue el SPSS versión 22 y para determinar el contraste de raíz unitaria de Dickey-Fuller aumentado fue el programa STATA versión 15.

Aspectos éticos

Los datos son de acceso público, abierto y anónimo, por lo que no se requirió aprobación de un comité de ética institucional.

RESULTADOS

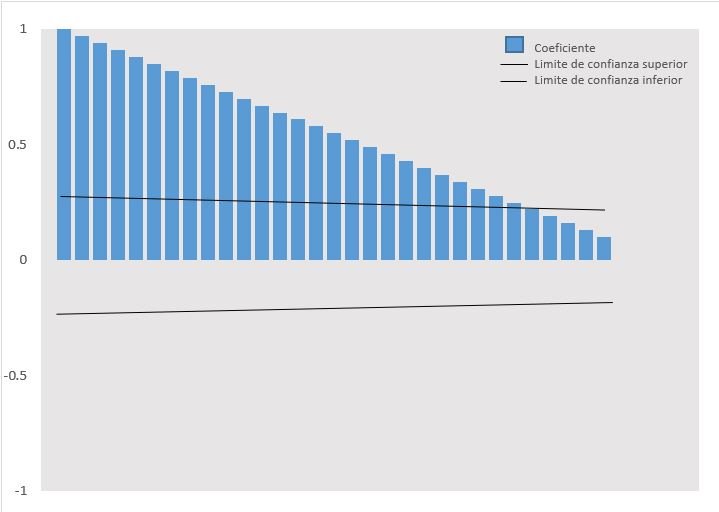
En la tabla 1, se observa el recuento diario de casos con COVID 19, entre el 6 de marzo de 2020 y 11 de junio de 2020. En la Figura 1, se muestra que los coeficientes de autocorrelación (ACF) decrecen lentamente en forma lineal, por lo que corresponden a una serie temporal no estacionaria, siendo esta corroborada por el contraste de raíz unitaria de Dickey-Fuller Aumentado (p>0,01).

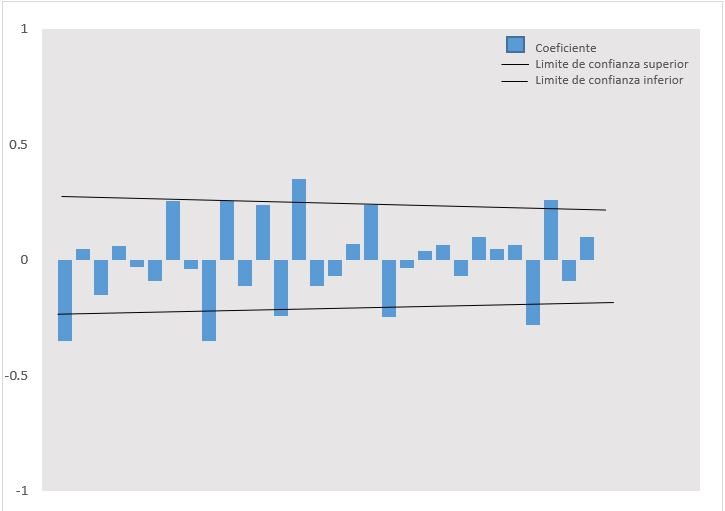
En la Figura 2 se muestra la transformación estacionaria de segundo orden, en la cual se estabilizo la serie temporal mediante la eliminación de tendencias y así obtener el modelo apropiado con las ordenes p, d, q, el cual fue ARIMA (0,2,9). En la Tabla 2 se muestra los parámetros (p, d, q) obtenidos en el proceso del modelado; el Criterio de Información Bayesiano Normalizado (BIC) que indica que 13,475 fue el valor más bajo obtenido indicando el mejor modelo ARIMA; el error porcentual medio absoluto (MAPE) que indica que el pronóstico del modelo está errado en un 7,775%; y la prueba de Ljung-Box que indica que el modelo es capaz de reproducir el patrón de comportamiento sistemático de la serie temporal.

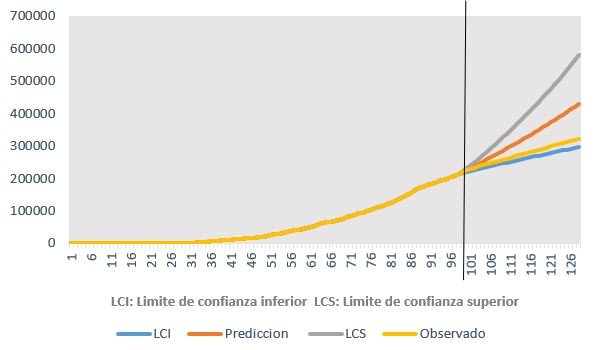
En la Figura 3 y Tabla 3 se muestra el pronóstico del número de casos con intervalos de confianza del 95% y los casos observados; desde el 12 de junio al 11 de julio de 2020, con los datos del 06 de marzo de 2020 al 11 de junio de 2020. Los valores de los casos observados, son inferiores a los valores de los casos pronosticados, encontrándose los observados dentro de los valores mínimo y máximo de los estimados.






DISCUSIÓN

Esta investigación se realizó para predecir el número de casos con COVID-19 desde el 12 de junio hasta el 11 de julio de 2020 en el Perú utilizando el método Autorregresivo Integrado de Medias Móviles (ARIMA), para posteriormente compararlos con los casos observados con el fin de buscar una aproximación entre ambos resultados.

Hay que tener en cuenta que los pronósticos obtenidos a partir de un modelo de serie temporal univariante, son extrapolaciones de los datos observados hasta el tiempo en que termina la serie, siendo en muchas ocasiones muy efectivas proporcionando un punto de referencia para predecir futuros valores de los casos confirmados. La mayoría de las series son estocásticas, en que el futuro solo se puede determinar parcialmente por sus valores pasados, por lo que los pronósticos exactos son imposibles ⁽²⁴⁾.

Diversos autores ^(1,11,15-20), a nivel mundial, han desarrollado modelos para el pronóstico de casos de COVID-19 basados en el método ARIMA, en los cuales han utilizado determinados estadísticos para evaluar la bondad de ajuste del modelo mostrando buenos resultados en cuanto a pronósticos a corto plazo.

El modelado realizado en este estudio ha seguido todas las etapas de la metodología de Box-Jenkins ^(11,22-23), con el fin de obtener el mejor modelo predictivo; y si bien algunos investigadores han aplicado estas etapas, solo han mencionado algunos parámetros estadísticos utilizados en su construcción.

Moftakhar L y Seif M⁽¹⁾, mencionan el uso del análisis de los coeficientes de autocorrelación (ACF), autocorrelación parcial (PACF) y el test de Box-Ljung; Singh RK et al⁽¹¹⁾, mencionan el uso del criterio de información de Akaike (AIC); Ceylan Z⁽¹⁵⁾, menciona el uso del error cuadrático medio (RMSE), error absoluto medio (MAE) y error porcentual medio absoluto (MAPE); Benvenuto D ⁽¹⁶⁾,menciona el uso del contraste de raíces unitarias de Dickey-Fuller Aumentado (ADF) y el análisis de los coeficientes de autocorrelación (ACF) y autocorrelación parcial (PACF); Yousaf M et al⁽¹⁷⁾, mencionan el uso del análisis de los coeficientes de autocorrelación (ACF) y autocorrelación parcial (ACF y PACF) y el criterio de información de Akaike (AIC); Hiteshi Tandon ⁽¹⁸⁾, menciona el uso del análisis de los coeficientes de autocorrelación (ACF) y autocorrelación parcial (PACF) además de la varianza, prueba de normalidad, el error porcentual medio absoluto (MAPE), la Desviación Absoluta de la Media (DAM) y la desviación cuadrática media (MSD); Rishabh Tyagi et al ⁽¹⁹⁾, mencionan el uso del análisis de los coeficientes de autocorrelación (ACF) y autocorrelación parcial (PACF), el contraste de raíces unitarias de Dickey-Fuller Aumentado (ADF), y proporciona los intervalos de confianza (IC) del 95% para las estimaciones puntuales; por ultimo Perone G ⁽²⁰⁾, menciona el uso del criterio de información de Akaike (AIC), el análisis de los coeficientes de autocorrelación (ACF) y autocorrelación parcial (PACF), el contraste de raíces unitarias de Dickey-Fuller Aumentado (ADF), la prueba modificada para raíz unitaria de Elliott-Rothenberg-Stock (DF-GLS), el error absoluto medio (MAE), la prueba de normalidad, la homocedasticidad, la prueba del multiplicador de Lagrange de Engle, y el test de Box-Ljun, muchos de los cuales coinciden con los utilizados en esta investigación.

Si bien es cierto que dentro de los modelos matemáticos de pronóstico existe una variedad de estos; el modelo ARIMA tiene una mayor precisión de ajuste que los demás ⁽²⁶⁾, ya que captura las tendencias de pronóstico estacionales y no estacionales; este estudio se centra en un modelo no estacional, para describir el patrón de crecimiento a lo largo del tiempo. Por otro lado, si un modelo utiliza enfoques estadísticos para su selección y evaluación; hay que reconocer que, si el número de casos no es cierto, al ser la única fuente de información oficial disponible en el país, puede conducir a un pronóstico inexacto. Aun con esta limitación, los resultados sugieren que el método puede ayudar a estimar la dinámica del brote y proporcionar pautas para detener o controlar de la mejor manera el aumento de las infecciones en el país, pero también es evidente, que todo intento de control, depende de las políticas públicas que se dicten por parte de las autoridades y sobre todo, la toma de conciencia de cada ciudadano sobre la propagación del COVID-19 y de los efectos letales que un comportamiento o practica irresponsable puede traer como consecuencia para sí mismo, su familia y la comunidad.

Asimismo, este modelo permite analizar la posible evolución de la curva de contagios y poder comparar los resultados con los de otros países para evaluar las acciones que se están tomando.

Cabe aclarar que esta estimación está fuertemente relacionada con la tendencia de los datos de la serie original, y el resultado de los pronósticos, pueden ayudar a entender cualquier cambio repentino en el pronóstico de casos COVID-19. Dentro de la limitación del estudio se puede mencionar, que la precisión del pronostico depende de la precisión de los datos aplicados, esto quiere decir que no hay alguna otra evidencia adicional que pueda estimar el número exacto de pacientes con COVID-19, ya que solo se consideró el numero de casos oficiales reportados por el Instituto Nacional de Salud y Centro Nacional de Epidemiologia, Prevención y Control de Enfermedades del Ministerio de Salud.

CONCLUSIÓN

Los resultados obtenidos con el modelo ARIMA, comparados con los datos observados, muestran un ajuste adecuado de los valores; y aunque este modelo, de fácil aplicación e interpretación, no simula el comportamiento exacto en el tiempo puede considerarse una herramienta simple e inmediata para aproximar el numero de casos.

---

---